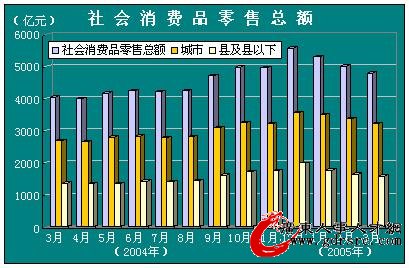
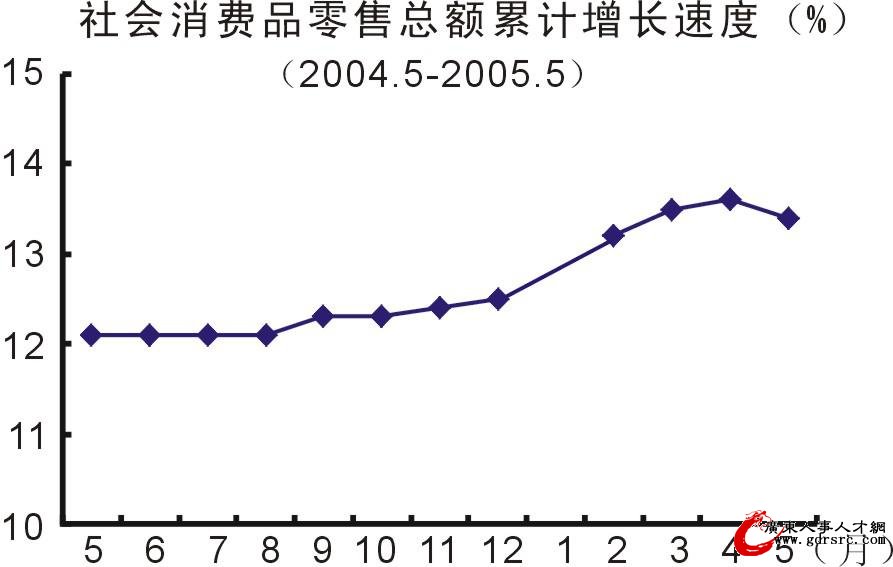
社会消费品零售总额

一季度全国社会消费品零售总额增长13.7%
　　一季度，社会消费品零售总额15112亿元，比去年同期增长13.7%。其中，3月份4799亿元，增长13.9%。 
　　分地域看，城市社会消费品零售额10090亿元，比去年同期增长14.7%；县及县以下零售额5022亿元，增长11.7%。 
　　分行业看，批发零售业社会消费品零售额12616亿元，比去年同期增长13.6%；餐饮业零售额2063亿元，增长17.2%；其他行业零售额433亿元，增长0.2%。 
分商品类别看，限额以上批发零售业吃、穿、用商品类零售额同比分别增长16.8%、18.9%和16.5%。建筑及装潢材料类增长23.3%，家用电器和音像器材类增长16.1%，洗涤用品类增长10.3%，文化办公用品类增长21.1%，服装鞋帽、针、纺织品类增长18.9%，化妆品类增长19.3%，金银珠宝类增长19.2%，体育、娱乐用品类增长24.8%，儿童玩具类增长12.8%，食品、饮料、烟酒类销售增长16.8%，肉禽蛋类增长25.7%，通讯器材类零售额增长19.7%，汽车类增长10.2%，石油及制品类增长37.5%。
 
 


 
 

 
 

 
 

 
 

 
 

 
 

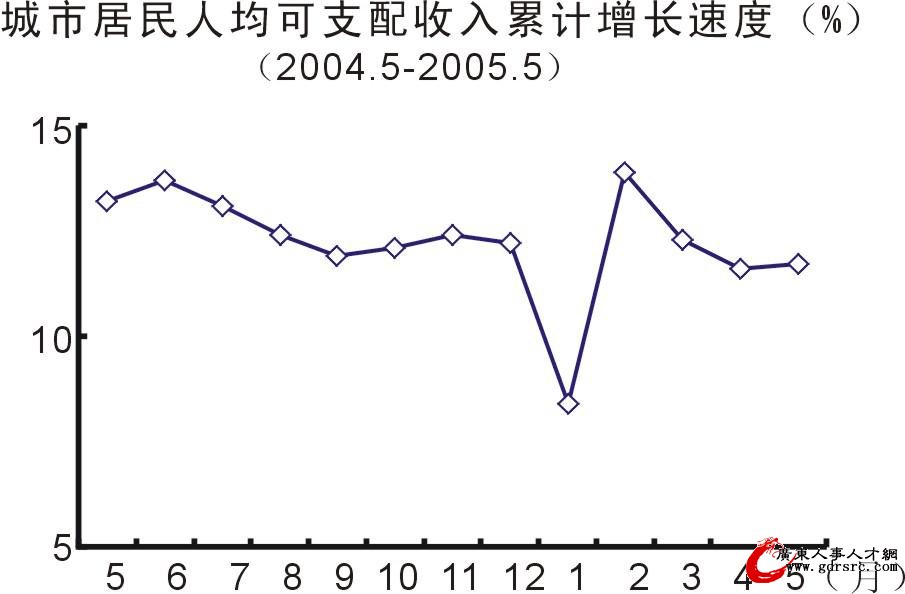
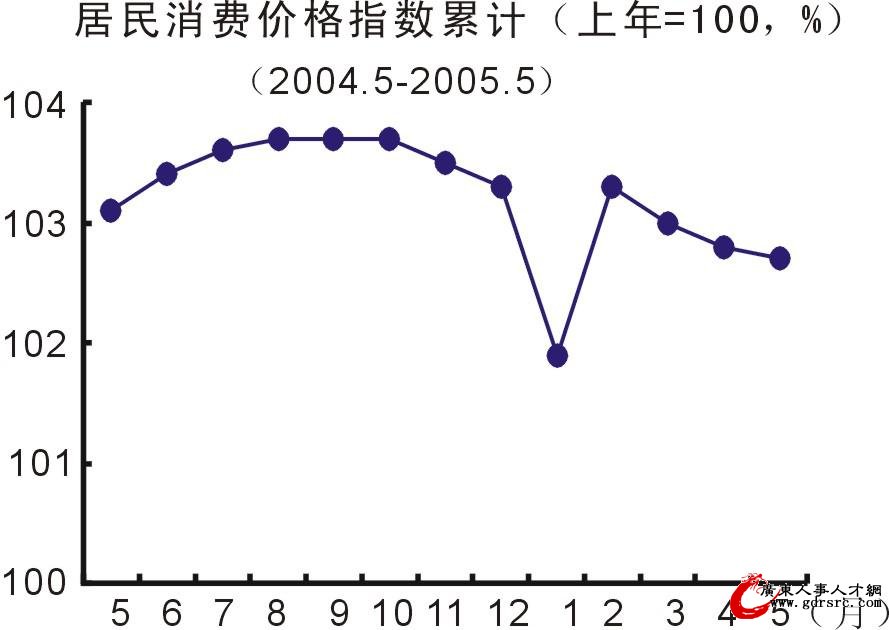
指数

指数是一种表明社会经济现象动态的相对数，运用指数可以测定不能直接相加和不能直接对比的社会经济现象的总动态；可以分析社会经济现象总变动中各因素变动的影响程度；可以研究总平均指标变动中各组标志水平和总体结构变动的作用。指数按所反映的现象范围不同，分为个体指数和总指数。前者反映个体经济现象变动的相对数，如个别产品的物量指数、个别商品的价格指数等；后者是表明全部经济现象变动的相对数，如工业总产值指数、居民消费价格总指数。
　　按所反映的现象性质的不同，分为数量指数和质量指数。前者反映生产、经营或经济活动数量的变动，如商品销售量指数；后者是说明经济活动质量变动的指数，如产品成本指数、劳动生产率指数。
　　按计算形式的不同，分为综合指数和平均数指数，前者指两个总量指标对比计算出来的指数，后者是前者的变形。
　　而一般的相对数，是两个有联系的指标的比值，它可以从数量上反映两个相互联系的现象之间的对比关系。相对数的种类很多，根据其表现形式可分为两类：一类是有名数，即凡是由两个性质不同而又有联系的绝对数或平均数指标对比计算所得的相对数，一般都是有名数，而且多用复合计量单位。另一类是无名数，无名数可以根据不同的情况分别采用倍数、成数、系数、百分数、千分数等来表示，如：人口出生率、死亡率等。相对数根据相互对比的指标的性质和所能发挥的作用不同，又可分为动态相对数、结构相对数、比较相对数、强度相对数、计划完成程度相对数等五种。
　　因此，指数和一般的相对数的区别在于：一般的相对数是两个有联系的现象数值之比，而指数却是说明复杂社会现象经济的发展情况，并可分析各种构成因素的影响程度。
 
 

农产品生产价格指数

农产品生产价格指数是反映一定时期内，农产品生产者出售农产品价格水平变动趋势及幅度的相对数。该指数可以客观反映全国农产品生产价格水平和结构变动情况，满足农业与国民经济核算需要。其中某代表品生产价格指数是通过对全部有出售该产品行为的调查单位的个体指数进行几何平均求得的，大、中、小类价格指数是通过对其所属的类（或代表品）的价格指数进行加权平均求得的。季度累计价格指数的计算方法与分季指数的计算方法相同。
 
农产品生产价格是指农产品生产者第一手（直接）出售其产品时实际获得的单位产品价格。农产品生产价格的提高意味着农民从单位产品中获得的收入增加，反之，则农民获得的收入减少。
 
 

个人所得税税率计算公式
级数 月 工资、薪金收入（a） 税率 应交税 0 不超过800元 不缴税 1 超过800元至1300元 5 a×5%－40
2 超过1300元至2800元 10 a×10%－105 3 超过2800元至5800元 15 a×15%－245 4 超过5800元至20800元 20 a×20%－535 5 超过20800元至40800元 25 a×25%－1575 6 超过40800元至60800元 30 a×30%－3615 7 超过60800元至80800元 35 a×35%－6655 8 超过80800元至100800元 40 a×40%－10695 9 超过100800元 45 a×45%－15735

“番”与“倍”

增加一倍，就是增加100％; 翻一番，也是增加100％。除了一倍与一番相当外，两倍与两番以上的数字含义就不同了。而且数字越大，差距越大。如增加两倍，就指增加200％；翻两番，就是400％(一番是二，二番是四，三番就是八)，所以说翻两番就是增加了300％，翻三番就是增加了700％。“番”是按几何级数计算的，“倍”是按算术级数计算的。
计算翻番公式为：
n＝[lg(报告期数÷基数)]÷lg2
n表示翻番数　lg是常用对数符号
 
 

“百分数”与“百分点”

　百分数是用一百做分母的分数，在数学中用“％”来表示，在文章中一般都写作“百分之多少”。百分数与倍数不同，它既可以表示数量的增加，也可以表示数量的减少。运用百分数时，也要注意概念的精确。如　“比过去增长20％”,即过去为100，现在是“120”;“比过去降低20％”，即过去是100，现在是“80”；“降低到原来的20％”，即原来是100，现在是“20”。运用百分数时,还要注意有些数最多只能达到100%,如产品合格率，种子发芽率等； 有些百分数只能小于100％，如粮食出粉率等；有些百分数却可以超过100％，如产品产量计划完成情况等。
　　“占”、“超”、“为”、“增”的用法，“占计划百分之几”指完成计划的百分之几；“超计划的百分之几”，就应该扣除原来的基数(－100％)；“为去年的百分之几”就是等于或相当于去年的百分之几；“比去年增长百分之几”应扣掉原有的基数（－100％）。
　　百分点是指不同时期以百分数形式表示的相对指标（如：速度、指数、构成等）的变动幅度。例如： 我国国内生产总值中，第一产业占的比重由1992年的20.8％下降到1993年的18.2％。
　　从上述资料中，我们可以说：国内生产总值中，第一产业占的比重，1993年比1992年下降3.6个百分点　（18.2－21.8＝－3.6）；但不能说下降3.6％。
 
 

在表述两个不同时期经济发展状况时，有时用增减百分比，有时用提高 或下降几个百分点，它们在计算方法和意义上有何不同？

增减百分比，是表述某一指标报告期水平比基期水平增加或减少的相对程度，是以百分比（%）表示的，其计算公式为： 
增（减）速度（%）= （某指标报告期数值-该指标基期数值）/该指标基期数值×100%
或 =某指标报告期数值 /该指标基期数值×100%-100% 
  上式表明，当报告期水平高于基期水平，比较后所得结果为增长百分比，就是增长速度；当报告期水平低于基期水平，比较后所得结果为减少百分比，就是下降速度。
  百分点则是百分比中相当于1%的单位，它是一个量词。它是分析百分比增减变动的一种表现形式。当两个百分数比较时，如果是用“和”或“差”表示的，称为百分点。例如，工业总产值今年的增长速度为19%，去年的增长速度为16%，今年比去年的增长幅度提高了3个百分点（19%-16%）；再如，今年物价上升了8%，去年物价上升了10%，今年比去年物价上升幅度下降了2个百分点（8%-10%）。百分点应用比较广泛，在特定场合中表示着特定的含义，如作为证券市场、外汇市场、储蓄利率的标准单位等。
 
 

在统计分析中经常使用的“贡献率”是什么含义？它是怎样计算的？

贡献率是分析经济效益的一个指标。它是指有效或有用成果数量与资源消耗及占用量之比，即产出量与投入量之比，或所得量与所费量之比。计算公式： 
贡献率（%）=贡献量（产出量，所得量）/投入量（消耗量，占用量）×100%
    贡献率也用于分析经济增长中各因素作用大小的程度。
计算方法是：
贡献率（%）=某因素贡献量（增量或增长程度）/总贡献量（总增量或增长程度）×100%
    上式实际上是指某因素的增长量（程度）占总增长量（程度）的比重。
举例说明如下：
总资产贡献率（%）=（利润总额+税金总额+利息支出）/平均资产总额×100%
（1）总资产贡献率：反映企业资金占用的经济效益，说明企业运用全部资产的收益能力。
（2）社会贡献率：是衡量企业运用全部资产为社会创造或支付价值的能力。
社会贡献率（%）= 社会贡献总额/平均资产总额×100%
    社会贡献总额包括工资、劳保退休统筹及其他社会福利支出、利息支出净额、应交增值税、产品销售税金及附加、应交所得税及其他税、净利润等。为了反映企业对国家所作贡献的程度，可按上述原则计算贡献率。
企业对国家的贡献率（%）= 税金总额+上缴利润/社会贡献总额×100%
    技术进步对产出增长速度的贡献率
    这个指标是指在产出增长速度中，技术进步因素所占的比重，综合反映了技术进步对经济增长作用的大小。
技术进步对产出增长速度的贡献率（%）=技术进步速度/产出增长速度 ×100%
    上式贡献率越大则表明技术进步对经济增长的贡献和作用就越大，反之则小。
（4）各产业贡献率：
    第一、二、三产业增量与国内生产总值增量之比，即为各产业的贡献率。
第三产业贡献率= 第三产业当年增量/国内生产总值当年增量×100%
    应该注意的是，贡献率指标比较抽象，在使用时，应说明具体含义，但也不能任意使用，要符合常规，做到标准化、规范化、通俗化。如资本收益率、资金利税率以及某些对增量因素分析的指标，已有专用名称，就没有必要改称为贡献率。另外，在计算各产业贡献率时应剔除价格变动因素，分子、分母均用可比价格的增量计算。