牛吃草问题的三种解法:
第一种,牛吃草问题周氏比例法第二种,方程法。
第三种,公式法。
所谓的列表法,就不介绍了,实质是公式法或方程法的模式化。
基本牛吃草
例1:有一块匀速生长的草场,27头牛6周可以吃完,或者23头牛9周可以吃完.若是21头牛,要几周才可以吃完?
A.10 B.11 C.12 D.15
第一种方法、周氏比例法解牛吃草问题:
步骤看起来很多,掌握了,实际上很容易 :)
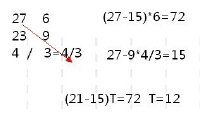
第一步:把前二次的牛头数,时间的数字分两列写出来。
27 6
23 9
第二步:每两列数字相减,把结果写出来。4 与 3
第三步:二个差相除。4/3
第四步:求X.三点一线,把三数联起来进行运算,图中红线。按A-B*C=27-9*4/3=15 算出结果X。
第五步:求Y.根据基本公式(牛-X)天=Y,代入其中一排数据,比如第一排(27-15)*6=72
第六步:求结果。把X,Y,代入提问中,求出答案。(21-15)T=72 T=12
心语:看到有些牛吃草题目,用列方程或公式,计算较繁,所以在今年6月份,为大家发明了这么一个解法,可避开一些计算,更快的算出答案。实质是用比例法的思想解题,把这个牛吃草的解法,归在周氏比例法的系统中。此解法,后来被人盗用,并说成是他原创。表示,的原创解法欢迎大家转载,传播,但希望能尊重原创者,引用时注明出处。
精剖牛吃草问题:我们看此题,典型的牛吃草问题。草,是在不断生长的,它有生长的效率;牛,在努力吃草,它有吃草的效率。
牛吃草问题可以理解成为工程问题。牛有吃草的效率,草有生长的效率,而这个草场原有草量,就相当于工程总量。
每天的实际效率=牛吃草的效率-草生长的效率。
工程总量=实际效率*时间=(牛吃草的效率-草生长的效率)* 时间
此题,我们知道牛的数量,但不知道牛的效率,工程总量(即原有草量)不知道,草的生长效率也不知道。题目缺乏条件,因为我们需要设值。假设每头牛每周吃1份草,假设草场每周长生草的效率是X份,设原有总草量是Y份
以上题为例:
第二种方法:公式法。
27头牛吃的总草量=27*1 * 6=
23头牛吃的总草量=23*1 *9=
它们同样吃完一个草场的草,可为什么27*6 不等于 23*9 呢?
原因在于它们吃的时间不同,草在不断生长,前者草只生长了6周,后者,草生长了9周。
27*1 * 6= 原有草量 + 草6周生长的量
23*1 *9= 原有草量 + 草9周生长的量
所以它们所吃的草量的差距,就等于9-6=3周草生长的量,那么每一周草生长量=(23*9 – 27*6)/(9-6)
(或从解方程的角度,直接把第二式减第一式,推出草每周生长率的公式)
所以,我们可总结出每周草生长量的公式:
X=(牛1*时间1 - 牛2*时间2) / (时间1-时间2)
(其实求Y,也有公式,这个等下在下文的电梯类牛吃草问题中跟大家介绍。)
公式法解题三步:
第一步,根据公式求出X。
第二步,根据牛吃草问题基本公式求出Y.
第三步,把X,Y代入问句,根据牛吃草基本公式,求出所问。
1、X=(23*9 –27*6)/(9-6)=15
2、Y=(23-15)*9=72
3、(21-15)T=72 T=12
提醒:在典型牛吃草问题中,吃草时间长的吃的总草量,总是大于吃草时间短的吃的总草量。比如这题 23*9〉27*6。因为吃的时间长,草生长的量也多。
第三种方法:方程法。
根据原工程总量=实际效率*时间=(牛吃草的效率-草生长的效率)* 时间
列方程:
(27*1 – X ) * 6 = Y
(23*1 – X ) * 9=Y
因为我们设每头牛每天吃1份,27头牛就是27份
即(27-X)* 时间6 = 原有草量Y
这也就是 (牛-X)* 时间=Y 这个牛吃草问题基本公式的来源。
这个基本公式,需牢记!
牛的头数 与 草每天的生长量,本来是不能直接相减的!
这里因为设牛每天吃一份,所以牛头数的数量才和这些个牛每天的效率的数字相同。
然后,解方程:
X=15
Y=(27-15)*6=72 代入其中一式。根据(牛-X)天 基本公式
(21-15)* T =72 代入问句。根据(牛-X)天 基本公式
T=12
例二:有一块匀速生长的草场,可供12头牛吃25天,或可供24头牛吃10天。那么它可供几头牛吃20天?
A.10 B.14 C.16 D.18
解析:
第一种方法:
12 25
24 10
12 / 15 =4/5
1.X=12-10*4/5=4
2.Y=(24-4)10=200
3.(N-4)20=200 N=14 选B.
第二种方法:
1. X=(25*12 – 24*10)/)(25-10)=4
2.Y=(24-4)10=200
3.(N-4)20=200 N=14 选B.
第三种列方程的解法,就不多说啦。