加法原理，表示并列关系；
        乘法原理，表示串联关系。　　
         加法原理和乘法原理的本质区别就是要区分里面到底是要分类，还是需要分步，如果是分类，那么必须用加法原理，如果是分步则需要用乘法原理。
　　概率公式：符合条件的情况数/总体情况数。
三、解题方法　　
       在解答排列组合问题的时候，我们只要是依据排列组合的公式，然后通过有效的分类，从而得到满足条件的情况数，在解题的时候，要能够做到合理分类，准确分 步。如果当在解答某些问题，正面入手情况复杂，不容易求解的时候，将试题从反面考虑，从而转化为一个较为简单问题的方法。　　
        对于比较特殊，或者说试题具有明显特征的，我们可以采用特定的解题方法，比如说如果要求某些元素必须相邻，那么这时我们就将这些元素看作是一个元素，然后与其他元素排列，从而得到正确结果，也就是采用捆绑法。　　
       如果当试题中出现特殊元素或者特殊位置的时候，我们就可以考虑采用优先法解答；如果当试题中要求某几个元素不相邻的时候，我们可以采用插空法。　　
       对于概率问题而言，我们主要是在依据排列组合问题的基础上，利用计算公式，从而得到试题的正确答案。
　　【真题示例1】某论坛邀请了六位嘉宾，安排其中三人进行单独演讲，另三人参加圆桌对话节目。如每位嘉宾都可以参加演讲或圆桌对话，演讲顺序分先后且圆桌对话必须安排在任意两场演讲之间，问一共有多少种不同的安排方式？　
            　A．120       B．240      C．480     D．1440　　
         【答案】B　　
         【解析】本题考查的排列组合问题。　　
          由 于其中三人参加演讲比赛，其顺序分先后，那么一共有P（6，3）=6×5×4=120种。由于是圆桌对话，每桌的人数应该大于等于2，现在有3人，那就只 能组成一桌，且必须安排在任意两场演讲之间，那么圆桌对话可以插在演讲形成的2个空中，则一共有120×2=240，故本题的正确答案为B选项。

　　【真题示例2】某科室共有8人，现在需要抽出两个2人的小组到不同的下级单位检查工作，问共有多少种不同的安排方案?　　
          A．210       B．260      C．420     D．840　　
       【答案】C　　
       【解析】本题考查的是排列组合问题。　　
        根 据题意，由于是到不同的下级单位，那么第一步，先从8人里面选取2人到一个下级单位，则有C（8，2）种方法；第二步，从剩余的6人里面，选取2人到另外 一个下级单位，则有C（6，2）种方法，根据乘法原理，则一共有C（8，2）×C（6，2）=410种安排方案，故本题的正确答案为C选项。
       【真题示例3】某单位有职工15人，其中业务人员9人。现要从整个单位选出3人参加培训，要求其中业务人员的人数不能少于非业务人员的人数，问有多少种不同的选法？　　     A．156      B．216      C．240     D．300　　
       【答案】D　　  
       【解析】本题考查的是排列组合问题。　　
        根据题意，由于一共选拔3人，且要求业务人员的人数不能少于非业务人员，那么可能的选拔情况为：2名业务人员+1名非业务人员；3名业务人员。　　
        第一类，如果是2名业务人员+1名非业务人员，则有C（9，2）×C（6，1）=36×6=216种选法；第二类，如果是3名业务人员，则有C（9，3）=84种选法；根据加法原理，则一共有216+84=300种不同的选法，故本题的正确答案为D选项。

　　【真题示例4】某市举办经济建设成就展，计划在六月上旬组织5个单位参观，其中1个单位由于人数较多，需要连续参观2天，其他4个单位只需参观1天。若每天最多只能安排一个单位参观，则参观的时间安排共有（   ）种。　　A．630B．700C．15120D．16800　　
       【答案】C　　
       【解析一】本题考查的是排列组合问题。　　
        由于有一个单位必须连续参观两天，那么我们把要求参观两天的单位的天数捆绑在一块，看作是1天，则试题就变成了在9天里面有5个单位参观，即有P（9，5）种，数值能被9整除，且较大，只有C选项符合。所以我们首先要分析这个单位。　　
       【解析二】根据题意，第一步，在六月上旬选择两天给这个单位，由于必须是连续的，则有以下可能（1，2）、（2，3）、（3，4）……（9，10），共9种可能；　　
        第二步，安排剩余的4个单位，在剩余的10-2=8天里面选择4天给这4个单位，并对其进行全排列，则有C（8，4）P（4，4）=8×7×6×5。　　
        根据乘法原理，则不同的安排方法有9×8×7×6×5，很明显这个数值能被9整除，排除B、D选项，且这个数值较大，那就排除A选项，故本题的正确答案为C选项。
       【真题示例5】 一个由4个数字（0~9之间的整数）组成的密码，每连续两位都不相同，问任意猜一个符合该规律的数字组合，猜中密码的概率为（    ）。　 　                   A．1/5040          B．1/7290         C．1/9000           D．1/10000　　
        【答案】B　　
        【解析】本题考查的是概率问题。　　
         根据题意，要求概率，那么最关键的是求出有多少种组合方法，如果4个数字的第一位确定，那么第2个数值，只能从剩余的9个里面选，以此类推，从而有满足条 件的组合数有C（10，1）C（9，1）C（9，1）C（9，1）=10×9×9×9，最后两位数为90，结合选项，只有B选项符合。

　　【真题示例6】小王和小张各加工了10个零件，分别有1个和2个次品。若从两人加工的零件里各随机选取2个，则选出的4个零件中正好有1个次品的概率为（    ）。　　A．小于25%       B．25%~35%      C．35%～45%       D．45%以上　　
       【答案】C　　
       【解析】本题考查的是概率问题。　　
        根据题意，在4个零件中抽中1个次品的情况有两种：（1）抽中小王制作的次品；（2）抽中小张制作的次品。总的抽取方式为C（10，2）×C（10，2）=45×45　　
       如果抽中小王制作的次品，则不同的抽取方法有C（9，1）×C（8，2），其抽取概率为9×4×7/（45×45）=28/225；如果抽中小张制作的次 品，则不同的抽取方法有C（9，2）×C（2，1）×C（8，1）=9×4×2×8，其抽取概率为9×64/（45×45）=64/225。那么总的概率 就为92/225，口算这个值略大于40%，故本题的正确答案为C选项。

第六章 容斥原理与抽屉问题


　 　容斥原理与抽屉问题，在这几年的国考是试题里面交替出现，也就是说今年考查了容斥原理，那么就不考查抽屉问题了，反之亦然，不过在2012、2013年 的国考试题里面，着重考查的是抽屉问题，因为这个知识点对于逻辑分析能力的要求更强，所以我们一定要熟练的掌握此种问题。
一、考点分析　　
       纵观历年的容斥原理的试题，难度不高，而且一般会是三集合的容斥原理，同时只要我们掌握了基本的公式，那么此类问题就是我们拿分的试题。　　
       出现频度：★★★★　　
       出题概率：★★★　　
       试题难度：★★　　
       抽屉问题，相对来说比较抽象，不过在解题的时候，主要有两种方法，一种是构造抽屉，一种就是最不利原则，在国考试题里面重点考查的是构造抽屉的方法。　　
       出现频度：★★★★　　
       出题概率：★★★★　　
       试题难度：★★★
二、基础知识　　
      1、两集合容斥原理：A∪B=A+B-A∩B。
      
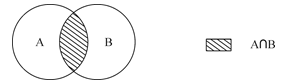
　　2、三集合容斥原理：A∪B∪C=A+B+C-A∩B-B∩C-A∩C+A∩B∩C。
      
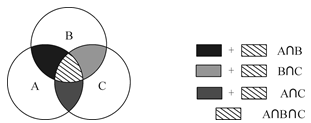
　　【注意】不论是三集合容斥原理，还是两集合容斥原理，其本质公式都是按照“重复两次，减一次；重复三次，减两次”的核心思想来的。
　　抽屉原理一：将多于n件物品任意放到n个抽屉中，则至少有一个抽屉中有不少于2件。　　
       抽屉原理二：把多于m×n件物品任意放到n个抽屉中，则至少有一个抽屉里有（m+1）件或多于（m+1）件的物品。
三、解题方法　　
       容斥原理的解题方法，主要是公式法以及文氏图两种，一般来说，我们在解答这类试题的时候，画出图形这样相对来说，比较直观，而且简单，考试的时候，可以大胆的采用此种方法。　　
       构造抽屉，就是我们在解题的时候，从题意出发，分清楚“物品”和“抽屉”，然后运用抽屉原理的基本形式来解答试题。　　
       “最不利原则”，使我们解答抽屉原理最常用的一种方法，这种方法指的是，当我们在计算的时候，从最坏的情况入手来分析满足条件的情况。
　　【