中山大学现代远程教育入学考试《数学》（高中起点升专科）
考试大纲

 
总 要 求
考生应理解和掌握中学数学基础知识、基本技能、基本方法，应注意各部分知识结构及知识间的内在联系。考查逻辑思维能力、运算能力、空间想象能力，以及运用所学数学知识和方法分析问题和解决问题的能力。为后继课程的学习作准备。
考试内容的知识要求和能力要求作如下说明：
    1、知识要求
    本大纲对所列知识提出了三个层次的不同要求，三个层次由低到高顺序排列，且高一级层次要求包含低一级要求。三个层次分别为：
    了解：要求考生对所列知识的含义有初步的认识，识记有关内容，并能进行直接运用。
    理解、掌握、会：要求考生对所列知识的含义有较深的认识，能够解释、举例或变形、推断，并能运用知识解决有关问题。
    灵活运用：要求考生对所列知识能够综合运用，并能解决较为复杂的数学问题。
   2、能力要求
    逻辑思维能力：会对问题进行观察、比较、分析、综合、抽象与概括；会用演绎、归纳和类比进行推理；能准确、清晰、有条理地进行表述。
    运用能力：理解算理，会根据法则、公式、概念进行数、式、方程的正确运算和变形；能分析条件，寻求与设计合理、简捷的运算途径；能根据要求对数据进行估计，能运用计算器进行数值计算。
    空间想象能力：能根据条件画出图形，根据图形想象出直观形象；能正确地分析出图形中基本元素及其相互关系；能对图形进行分解、组合、变形。
    分析问题和解决问题的能力：能阅读理解对问题进行陈述的材料；能综合应用所学数学知识、思想和方法解决问题，包括解决在相关学科、生产、生活中的数学问题，并能用数学语言正确地加以表述。

• 复习考试内容

第一部分 代 数
（一）函数

1. 了解集合的意义及其表示方法。了解空集、全集、子集、交集、并集、补集的概念及表示方法，了解符号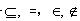的含义，并能运用这些符号表示集合、元素与集合的关系。
2. 理解函数概念，会求一些常见函数的定义域。
3. 理解函数的单调性和奇偶性的概念，掌握增函数、减函数、减函数及奇函数、偶函数的图像特征。
4. 理解一次函数、反比例函数的概念，掌握它们的图像和性质，会求它们的解析式。
5. 理解二次函数的概念，掌握它的图像和性质以及函数 y=aχ²+bχ+c(a≠0)与y=aχ² (a≠0)的图像间的关系；会求二次函数的解析式及最大值或最小值。能灵活运用二次函数的知识解决有关问题。
6. 了解反函数的意义。会求一些简单函数的反函数。

7、理解指数函数、对数函数的概念，掌握它们的图像和性质，会用它们解决有关问题。
（二）不等式和不等式组

1. 理解不等式的性质。

会用不等式的性质和基本不等式  a² ≥0(a∈R)   a²+b²≥2ab(a、b∈R)、 a+b≥2√ab （a、b≥0）解决一些简单问题。

1. 会解一元一次不等式，一元一次不等式组和可化为一元一次不等式组的不等式，会解一元二次不等式，了解区间的概念，会在数轴上表示不等式或不等式组的解集。

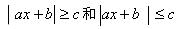3、了解绝对值不等式的性质，会解形如 的绝对值不等式。
   （三）数列

1. 了解数列及其有关概念。
2. 理解等差数列、等差中项的概念，会灵活运用等差数列的通项公式、前n项和公式解决有关问题。
3. 理解等比数列，等比中项的概念，会用等比数列的通项公式、前n项和公式解决有关问题。

（四）复数
1、理解复数与复平面的有关概念，会用向量表示复数。
2、了解复数的三角形式，会进行复数的代数形式与三角形式的互化。
3、会进行复数的代数形式的加、减、乘、除运算，会进行复数的三角形式的乘、除、乘方、开方运算。
4、会在复数集中解实系数一元二次方程。
（五）导数
1、了解函数极限的概念，了解函数极限的四则运算法则，了解函数连续的意义。
2、理解导数的概念及其几何意义。
3、会用基本导数公式（c, x^m(m为有理数)，e^x, lnx的导数），掌握两个函数和、差、积、商的求导法则。
4、理解极大值、极少值、最大值、最小值的概念，并运用导数求有关函数的单调区间、极大值、极少值及闭区间上的最大值和最小值。
5、会求有关曲线的切线方程，会用导数求简单实际问题的最大值和最小值。
 
第二部分 三角
（一）三角函数及其有关概念
1、了解正角、负角、零角的概念，理解象限角和终边相同的角的概念。
2、理解弧度的概念，会进行弧度与角度的换算。
3、理解任意角三角函数的概念。识记三角函数在各象限的符号和特殊角的三角函数值。
（二）三角函数式的变换
1、掌握同角三角函数间的基本关系式，诱导公式，会用它们进行计算、化简和证明。
2、掌握两角和、两角差、二倍角的正弦、余弦、正切的公式，会用它们进行计算、化简和证明。
（三）三角函数的图像和性质
1、掌握正弦函数，余弦函数的图像和性质，会用这两个函数的性质（定义域、值域、周期性、奇偶性和单调性）解决有关问题。
2、了解正切函数的图像和性质。
3、了解函数y＝Asin x y ＝sin(χ+φ) 、 y＝sin ωχ、 y＝Asin(ωχ+ φ ) 与 y＝sin χ 的图像之间的关系，会用“五点法”画出它们的简图，会求函数y＝Asin(ωχ+φ)的周期、最大值和最小值。
4、会由已知三角函数值求角，并会用符号 arcsin χ、arccos χ、arctan χ 表示。
（四）解三角形
1、掌握直角三角形的边角关系，会用它们解直角三角形及应用题。
2、掌握正弦定理、余弦定理，会用它们解斜三角形及简单应用题，会根据三角形两边及其夹角求三角形的面积。
  
第三部分 平面解析几何

• 平面向量
  1. 理解向量的概念，掌握向量的几何表示，了解共线向量的概念。
  2. 掌握向量的加、减法运算。掌握数乘向量的运算。了解两个向量共线的条件。
  3. 了解平面向量的分解定理。掌握直线的向量参数方程。
  4. 掌握向量数量积运算，了解运算的几何意义。了解向量数量积运算在处理长度、角度及垂直问题的应用。掌握向量垂直的条件。
  5. 掌握向量的直角坐标及其运算。

6、掌握平面内两点间的距离公式、线段的中点公式和平移公式。

• 直线
  1. 理解直线的倾斜角和斜率的概念，会求直线的斜率。
  2. 会求直线方程，能灵活运用直线方程解决有关问题。                    

3、掌握两条直线平行与垂直的条件以及点到直线的距离公式，会用它们解决有关问题。了解两直线所成角的公式。

• 圆锥曲线
  1. 了解曲线和方程的关系，会求两条曲线的交点。
  2. 了解充分条件、必要条件、充分必要条件的概念。
  3. 掌握圆的标准方程和一般方程以及直线与圆的位置关系，能灵活运用它们解决有关问题。
  4. 理解椭圆、双曲线、抛物线的概念，掌握它们的标准方程和性质，能灵活运用他们解决有关问题。
  5. 了解坐标轴的平移公式，会用平移公式化简圆锥曲线方程。

6、了解参数方程的概念、理解圆和椭圆的参数方程。
第四部分 立体几何
（一）直线和平面
1、了解平面的基本性质。
2、了解空间两条直线的位置关系以及异面直线所成角的概念。
3、了解空间直线和平面的位置关系。了解直线和平面垂直的概念，点到平面距离的概念。理解直线和平面平行、垂直的判定定理和性质定理。
4、了解点、斜线和斜线段在平面内射影、直线和平面所成角的概念。了解三垂线定理及其逆定理。
5、了解空间两个平面的位置关系以及二面角、二面角的平面角、两平行平面距离的概念。了解两平面平行、垂直的判定定理和性质定理。
    （二）空间向量
1、了解空间向量的概念、掌握空间向量的加法、减法和数乘向量的运算。掌握向量平移。
2、解空间向量分解定理。理解直线的方向向量。掌握直线的向量参数方程。
3、掌握空间数量积的定义及其运算。
4、会用向量运解决空间中的平行、垂直、夹角和距离等简单几何问题。
（三）多面体和旋转体

1. 了解直棱柱、正棱柱和平行六面体的概念，性质，会计算它们的表面积和体积。
2. 解棱锥、正棱锥的概念、性质，会计算它们的表面积和体积。
3. 了解圆柱、圆锥的概念，性质，会计算它们的表面积和体积。
4. 解球的概念、性质，会计算球面面积和球体体积。

第五部分 概率与统计初步
（一）排列、组合和二项式定理
1、了解分类计算原理和分步计数原理。
2、会解排列、组合的意义，掌握排列数、组合数的计算公式。
3、会解排列、组合的简单应用题。
4、了解二项式定理、会用二项展开式的性质和通项公式解决简单问题。
    （二）概率与统计初步
1、了解随机事件及其概率的意义。
2、了解等可能性事件的概率的意义，会用计算方法和排列组合基本公式计算一些等可能性事件的概率。
3、了解互斥事件的意义，会用互斥事件的概率加法公式计算一些事件的概率。
4、了解相互独立事件的意义，会用相互独立事件的概率乘法公式计算一些事件的概率。
5、会计算事件在n 次独立重复试验中恰好发生r 次的概率。
6、了解总体和样本的概念，会计算样本平均数和样本方差。
7、了解离散型随机变量及其期望的意义，会根据离散型随机变量的分布列求出期望值。
8、了解线性回归的方法极其简单应用。

• 考试形式及试卷结构

考试形式
闭卷，笔答。
全卷满分为100分，考试时间为120分钟。
   试卷结构

• 试卷内容比例  

代数 约40％      三角 约15％     平面解析几何 约20％ 
立体几何 15％    概率与统计约 10％

• 题型比例   

选择题 约50％    填空题 约10％   解答题（包括证明题） 约40％

• 试题难易比例 

较容易题 约30％  中等难度题  约50％  较难题 约20％