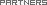Ａ．２０ Ｂ．３０ Ｃ．４０ Ｄ．５０
解析：
设全组最多a人‘
则 75a-（5个人分数）=70*（a-5）
要想a最大 则5个人分数总的为500(化简去看) 所以求得a=30
2 火车通过560米长的隧道用20秒,如果速度增加20%，通过1200米地隧道用30秒。火车的长度是多少米？
A220 B240 C250 D260
解析一：
速度比是 5:6 则时间比是6:5 通过1200现在时间是30
如果不提速时间是 36秒
则火车速度是 (1200-560)/16=40
则火车长度是 20*40-560=240
解析二：
速度比是 5:6 时间比是 2：3 则路程比是 10：18=5:9
4个比例点相差的是 1200-560=640 一个点是 640/4=160
则原来总的是 160*5=800 火车长度是 800-560=240
3 A、B两地之间有条公路，甲步行从A地去B地，乙骑摩托车从B地出发不停地往返于A、B两地之间。若他们同时出发，前后速度保持不变，60分钟后两人第一次相遇，70分钟后乙第一次超过甲。当甲到达B地时，两人迎面相遇过几次？（ ）
A.4 B. 5 C. 6 D. 7
解析一：
A--------C-----------------------B
A-------C------D--------------B
第一次相遇在C点相遇，第二次在D点
乙从C--àA-------D只要10分钟
甲从C-àA------D要60+60+10=130分钟
甲与乙的速度比是 1:13 则甲走完 乙走13圈 走两圈迎面来一次 所以选D
解析二：
70（V甲-V乙）=60（V甲+V乙）
V甲：V乙=1:13
甲与乙的速度比是 1:13 则甲走完 乙走13圈 走两圈迎面来一次 所以选D
4 甲、乙、丙、丁四个人站成一排，已知：甲不站在第一位，乙不站在第二位，丙不站在第三位，丁不站在第四位，则所有可能的站法数为多少种？
A6 B12 C9 D24
解析：
1 2 3 4
假如 乙 甲
丙
丁
假如第一位确定了，第二位就有三种选择，其余就可以确定 所以答案是 3*3=9
5 甲乙双方第一次用30元/千克的价格购买一批材料， 到第二次购买时， 价格涨到了40元/千克，已知甲每次购买10000千克， 乙每次用10000元购买， 则甲乙双方这两次交易的平均价格差约为（）元/千克？
A 0.5 B 0.7 C 1.5 D1.8
解析：
甲是 直接就知道是 35（ (30*10000+40*10000)/20000=35 ）
乙是调和平均数 30*40*2/(30+40)=240/7=34.3
所以答案是 35-34.3=0.7
或者式子交叉
30 a-40
a
40 30-a
因为单价比是 3:4 钱一样 所以个比是4:3
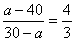a=240/735-34.3=0.7
6 甲、乙两人在一条90米的直路上来回跑步，甲的速度3米/秒，乙的速度2米/秒。如果他们同时分别从直路的两端A、B两点出发，当他们跑12分钟，共相遇了多少次？（从出发后两人同时到达某一点算作一次相遇）
解析：
算一个 3*12*60/90=24
但由于在端点相遇 有 90 180 180 180 四次
所以是24-4=20
7 A,B,C为三种酒精溶液。按质量比2：6：1混合，质量分数为30%；4：5：1混合时，为28%；6：1：1混合时，为25%。现缺少C种溶液，需要配置大量28%的溶液需要A和B的质量比是
A1：2 B1：3 C1：4 D1：5
解析：
30 3 36
28
25 2 24
所以8a+24b+4c=36
18a+3b+3c=24
所以 26:27:7 4:5:1=28:35:7
所以 2A=8B 选C
8 现有1角、2角、5角、1元、2元、5元、10元、20元、50元人民币各一张，100元人民币2张，从中至少取一张，共可组成不同的币值种数是（ ）(A)1024种 (B)1023种 (C)1536种 (D)1535种
解析：
每种都有2种可能，可取可不取，但是100元是两张，有100 200 0 三种选择，还有一种是全部不要，这种要减去
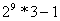通过尾数法 肯定选D9. 3位男生和3位女生共6位同学站成一排，若男生甲不站两端，3位女生中有且只有两位女生相邻，则不同排法的种数是（ ）
