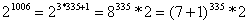
所以余数是 2
40. 树上结满了桃子,小猴第一天吃掉树上桃子的3/5,还扔掉了2个,第二天吃掉的桃子数再加上4个就等于第一天所剩桃子数的3/8,此时树上至少还有( )桃子。
,此时树上至少还有( )桃子。
A. 12个 B. 28个 C. 16个 D. 14个
解析:
假如余下的是A 通过最后一句话可以知道 A-4 占的是5/8 肯定是5的倍数,选D
41. 某市至旱季水源不足,自来水公司计划在下周七天内选择两天停止供水,若要求停水的两天不相连,则自来水公司共有()种停水方案。
A. 21 B. 19 C. 15 D. 6
解析:
6*5/2=15
42. 有一行人和一骑车人都从A向B地前进,速度分别是行人3.6千米/小时,骑车人为10.8千米/小时,此时道路旁有列火车也由A地向B地疾驶,火车用22秒超越行人,用26秒超越骑车人,这列火车车身长度为( )米。
A.232 B.286 C.308 D.1029.6
解析:
这题可以直接秒 肯定是11 13的倍数 选B
比例法: 时间比是11:13 则速度比是 13::11 和速度相差的是 7.2
两个点7.2 则 3.6*13*22/3600*1000=13*22=286
选B
43. 某科研单位欲拿出一定的经费奖励获奖的科研人员,第一名可得到全部奖金的一半多1万元,第二名可得到剩余的一半多1万元,以此类推都得到剩余奖金的一半多1万元,若到第七名恰好将奖金分完,则该单位需要拿出奖金( )万元。
A.156 B.254 C.256 D.512
解析:
假设原来的是A
第一个人拿完后 剩的是 A/2-1 这个数字肯定要被2整除
说明A/2 是个奇数,所以答案选B
44. 运动会上100名运动员排成一列,从左向右依次编号为1-100,选出编号为3的倍数的运动员参加开幕式队列,而编号为5的倍数的运动员参加闭幕式队列。问既不参加开幕式又不参加闭幕式队列的运动员有多少人?()
A.46 B.47 C.53 D.54
解析:
3的倍数有 100/3=33个
5的倍数有 100/5=20个
3的倍数 5的倍数有 100/15=6
所以是 33+20-6=100-A A=53
45. 三个快递员进行一堆快件的分拣工作,乙和丙的效率都是甲的1.5倍。如果乙和丙一起分拣所有的快件,将能比甲和丙一起分拣提前36分钟完成。问如果甲乙丙三人一起工作,需要多长时间能够完成所有快件的分拣工作?()
A.1小时45分 B.2小时 C.2小时15分 D.2小时30分
解析:
甲效率是2 乙是3 丙是3
乙丙与甲丙的效率比是 6:5 时间比是5:6
一个点36,则乙丙时间是 36*5=180 则总的是 180*6=1080
所以时间是 1080/8=135 所以选C
46.某公司要在长、宽、高分别为50米、40米、30米的长方体建筑的表面架设专用电路管道联接建筑物内最远两点,预设的最短管道长度介于:
A. 70—80米之间 B. 60—70米之间
C. 90—100米之间 D. 80—90米之间
解析:
最短的是 70 50 就是 (4900+2500)的根号 就是7400根号。肯定小于90 大于80 所以选D
47. 做一项工程,甲队单独做,需要30天完成,乙队单独做,需要21天完成。如果两队合作,由于彼此施工有影响他们的工作效率就要降低,甲队的工作效率是原来的六分之五,乙队工作效率只有原来的三分之二。现在计划18天完工,且要求两队合作天数尽可能少,那么两队要合作多少天?
A. 9 B. 10 C. 12 D.15
解析:
( 特值法 ) 设总的是 210
则甲的效率是 7 乙的效率是10
降低的效率是 35/6 乙是 20/3 甲乙合作的效率是 35/6+20/3=25/2
假设全部是 合作则做了 25/2*18=225 多了 225-210=15
要想合作的最少 则不合作的多 那么全部乙做 则就是 15/2.5=6
所以合作的是 18-6=12天
48. 甲乙两人从P、Q两地同时出发相向匀速而行,5小时后于M点相遇。若其他条件不变,甲每小时多行4千米,乙速度不变,则相遇地点距M点6千米;若甲速度不变,乙每小时多行4千米,则相遇地点距M点12千米,则甲乙两人最初的速度之比为?
A.2:1 B.2:3 C.5:8 D.4:3
解析:
P----------A----------M------------B-----------C-----------Q
12 6 14
当甲提速5小时后,走到的是C,则BC是 4*5-6=14
因为甲提速后于乙是在 B相遇 5小时是M相遇
所以当过了B点后 甲走14的时间与乙走的6时间是相同的
所以甲提速后于乙的速度比是 14:6=7:3 和速度是10
当乙提速4时 他们的和速度是相同的 也是10
同理 甲与乙提速的比是12:8
甲与乙提速的速度比是 6:4
所以甲乙不提速 的比是 6:3 是2:1 所以选A
49. 1.某晚会计划设置抽奖环节,能用于购买奖品的总金额固定,且要求每名一等奖奖品的金额是二等奖的两倍,每名二等奖奖品的金额是三等奖的两倍。如果一、二、三等级各设置两名,则一等奖奖品金额为每名720元。若一等奖设一名、二等奖两名、三等奖四名,则一等奖的奖品金额为每名( )元。
A. 780 B. 840 C. 880 D. 940
[答案]B
解析:(一)若各设两名,则二等奖金额为360,三等奖金额为180,总金额为(720+360+180)×2=2520(元)。改变设奖数量后,假定三等奖金额为X,则可得4X+2X·2+4X=2520,解得X=210,于是一等奖的奖品金额为840元。
(二)原来奖金人数分布为2,2,2,后来奖金人数分布为1,2,4 奖金比例为1比1比1,这里一等奖少了1人,三等奖多了二人,把一等奖的720快,拿一部分先分给多出来的三等奖的2个人,要分掉(720/4)*2=360元,即能做到一二三等奖3部分的奖金比例一样,再把多出的360平均分给3各部分,360/3=120即一等奖分到120元,720+120=840元
(三)原来奖金人数是2:2:2,奖金比是4:2:1,总的是8:4:2
现在人数比是1:2:4,那么总的比是 4:4:4
因为总资金是一样的,可以写成8:4:2=12:6:3, 4:4:4=7:7:7
那么6份对应的是720,那么7份就是 120*7=840
50.一个三口之家的年龄之和为99,其中,母亲年龄比父亲年龄的