真题示例1】某班对50名学生进行体检，有20人近视，12人超重，4人既近视又超重。该班有多少人既不近视又不超重?　　
                          A．22人      B．24人      C．26人      D．28人　　
       【答案】A　　
       【解析】本题考查的是容斥原理。　　
        根据题意以及容斥原理的公式，从而有该班既不近视又不超重有50-20-12+4=22，故本题的正确答案为A选项。

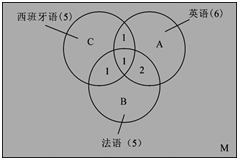
　　【真题示例2】某工作组有12名外国人，其中6人会说英语，5人会说法语，5人会说西班牙语；有3人既会说英语又会说法语，有2人既会说法语又会说西班牙语，有2人既会说西班牙语又会说英语；有1人这三种语言都会说。则只会说一种语言的人比一种语言都不会说的人多（    ）。　　
                   A．1人       B．2人       C．3人     D．5人　　
       【答案】C　　
       【解析】本题考查的是三集合容斥原理。　　
        根据题意，这个题目之间的关系比较复杂，所以我们最好采用画图的方法来解答。　　
        假设A——会说英语的人数，6；B——会说法语的人数，5；C——会说西班牙语的人数，5；A∩B∩C——三种语言都会的人是1人。　　
        由于A∩B——会说英语和法语的人数，3，那么只能说英语和法语的人有3-1=2；　　
        B∩C——会说法语和西班牙语的人数，2，那么只能说法语和西班牙语的人有3-2=1；　　
        A∩C——会说西班牙语和英语的人数，2，那么只能说西班牙语和英语的人有3-2=1。　　
        那么只会说英语的人有6-1-1-2=2，只会说西班牙语的有5-1-1-1=2，只会说法语的有5-1-1-2=1，所以只会一种语言的有2+2+1=5；　　
        一种语言都不会的人有12-5-1-1-2-1=2人，那么会一种语言的比不会任何一种语言的多5-2=3，故本题的正确答案为C选项。
【真题示例3】 小明和姐姐用2013年的台历做游戏，他们将12个月每一天的日历一一揭下，背面粘上放在一个盒子里、姐姐让小明一次性帮她抽出一张任意月份的30号或者 31号。问小明一次至少应抽出多少张日历，才能保证满足姐姐的要求？　　A．346       B ．347      C．348     D．349　　
    【答案】C　　
    【解析】本题考查的是抽屉问题。　　
     根据题意，由于2013年是平年，则一共有365张日历，其中30、31号的一共有11+7=18张，则需要抽出365-18+1，也就是尾数为8的数值才行，结合选项，选择C选项。

　　【真题示例4】某单位组织党员参加党史、党风廉政建设、科学发展观和业务能力四项培训，要求每名党员参加且只参加其中的两项。无论如何安排，都有至少5名党员参加的培训完全相同。问该单位至少有多少名党员？　　A.．17      B．21     C．25     D．29　　
       【答案】C　　
       【解析】本题考查的是抽屉原理。　　
        根据材料，每位党员能参加的课程一共有C（4，2）=6种不同的组合，由于至少5名党员参加的培训完全相同，则至少有党员6×（5-1）+1=25。故本题的正确答案为C选项。

　　【真题示例5】从1，2，3，……，30这30个数中，取出若干个数，使其中任意两个数的积都不能被4整除。问最多可取几个数?　　A．14个B．15个C．16个D．17个　　
       【答案】C　　
       【解析】本题考查的是抽屉原理。　　
        根 据题意，如果被4整除，那么必然要求其中的一个数值能被4整除，或者两个数值能被2整除即可。　　由于要求最多情况，那我们就考虑最不利因素，就是先把奇 数取出来，任意的数值的乘积必然不能被4整除，然后再取一个不能被4整除的偶数，也满足条件，那么最终满足条件的共有16个，故本题的正确答案为C选项。