解析：首先求出路上用去的时间，因为从家出发和回到家时，钟的时间是知道的，虽然它不准，但是用回到家的时间减出发时的时间就得到在路上与在图书馆一共花去的时间，然后再减去在图书馆花掉的1个半小时就得到路上花去的时间，除以2就得到从图书馆到家需要的时间。由于图书馆的8:50是准确时间，用这个时间加上看书的1个半小时，再加上路上用去的时间就得到了回到家时的准确时间，应该按这个时间来调整闹钟。
     所以：从家到图书馆的时间是：(4小时40分-1个半小时)/2=1小时35分, 所以到家时的准确时间是8:50+1个半小时+1小时35分=11:55, 所以到家时应该把钟调到11:55.
 
 
22. 某商店实行促销，凡购买价值200元以上的商品可优惠20%，那么用300元在该商店最多可买下价值（）元的商品
A.350   B.384   C.400   D.420
解析：优惠20%，实际就是300元×（1-20%），所以300元最多可以消费375元商品(300/0.8=375)，A选项中350<375，说明可以用300元来消费该商品，而其他选项的商品是用300元消费不了的，因此选A。
 
 
23. 20加上30，减去20，再加上30，再减去20，……至少经过多少次运算，才能得到500？
解析：加到470需要（470-20）/（30-20）=45次加和减，一共是90次，然后还需要1次加30就能得到500，一共是91次
 
 
24. 1913 ，1616 ，1319 ，1022 ，（）
A.724     B.725     C.526    D.726
解析：1913，1616，1319，1022每个数字的前半部分和后半部分分开。即将1913分成19，13。所以新的数组为，（19，13），（16，16），（13，19），（10，22），可以看出19，16，13，10，7递减3，而13，16，19，22，25递增3，所以为725。
 
 
25. 1 ，2/3 ，  5/9 ，( 1/2 ) ， 7/15 ， 4/9 ，4/9  
A.1/2     B.3/4     C.2/13       D.3/7
解析：1/1 、2/3 、 5/9、1/2 、7/15、4/9、4/9=>规律以1/2为对称=>在1/2左侧，分子的2倍-1=分母；在1/2时，分子的2倍=分母；在1/2右侧，分子的2倍+1=分母
 
 


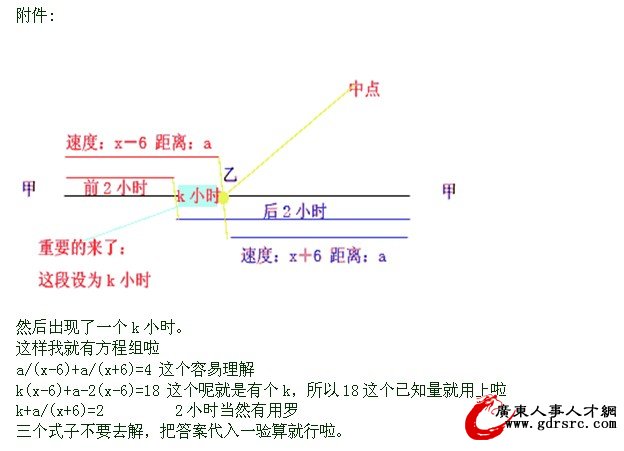
由a知x，由ax知k，最后看axk符合第三式就ok啦
a是距离，就是我们要求的解
为什么是X—6？？解释一下，
顺水比逆水快两倍的水速。
已知快12，那么水速就是6。
顺水＋6，逆水－6，ok？
 
 
27. 甲、乙、丙三艘船共运货9400箱，甲船比乙船多运300箱，丙船比乙船少运200箱。求三艘船各运多少箱货？
解析：根据已知甲船比乙船多运30O箱，假设甲船同乙船运的一样多，那么甲船就要比原来少运300箱，结果三船运的总箱数就要减少300箱，变成（9400－300）箱。 又根据丙船比乙船少运200箱，假设丙船也同乙船运的一样多，那么丙船就要比原来多运200箱，结果三船总箱数就要增加200箱，变成（9400－300＋200）箱。 经过这样调整，三船运的总箱数为（9400－300＋200）。根据假设可知，这正好是乙船所运箱数的3倍，从而可求出动船运的箱数。
乙船运的箱数知道了，甲、丙两船运的箱数马上就可得到。
 
 
28. 有50名学生参加联欢会，第一个到会的女同学同全部男生握过手，第二个到会的女生只差一个男生没握过手，第三个到会的女生只差2个男生没握过手，以此类推，最后一个到会的女生同7个男生握过手。问这些学生中有多少名男生？
解析：这是和差问题。我们可以这样想：如果这个班再多6个女生的话，最后一个女生就应该只与1个男生握手，这时，男生和女生一样多了，所以原来男生比女生多（7－1）6个人！男生人数就是：（50＋6）÷2＝28（人）。
 
 
29. 在一个两位数之间插入一个数字，就变成一个三位数。例如：在72中间插入数字6，就变成了762。有些两位数中间插入数字后所得到的三位数是原来两位数的9倍，求出所有这样的两位数。
解析：对于这个题来说，首先要判断个位是多少，这个数的个位乘以9以后的个位还等于原来的个位，说明个位只能是0或5！先看0，很快发现不行，因为20×9=180，30×9=270，40×9=360等等，不管是几十乘以9，结果百位总比十位小，所以各位只能是5。略作计算，不难发现：15，25，35，45是满足要求的数
 
 
30. 1009年元旦是星期四，那么1999年元旦是星期几？
A.四    B.五    C.六    D.七
解析：有240个闰年（1100，1300，1400，1500，1700，1800，1900不是闰年）。
每个元旦比上一年的星期数后推一天，
闰年的话就后推两个星期数
990/7余3，240/7余2
3+2=5
 
 
31. 5 ，5 ，14 ，38 ，87 ,（ ）
A.167    B.168   C.169    D.170
解析：前三项相加再加一个常数×变量
（即：N1是常数；N2是变量，a+b+c+N1×N2）
5+5+14+14×1=38
38+87+14+14×2=167
 
32.（ ） ， 36 ，19 ，10 ，5 ，2
A.77     B.69     C.54     D.48
解析：5-2=3 10-5=5 19-10=9 36-19=17
5-3=2 9-5=4 17-9=8
所以X-17应该=16
16+17=33 为最后的数跟36的差 36+33=69
所以答案是 69
 
 
33. 1 ，2 ，5 ，29 ，（）
A.34    B.846    C.866   D.37
解析：5=2^2+1^2
      29=5^2+2^2
      ( )=29^2+5^2
      所以( )=866,选c
 
 
34. -2/5 ，1/5 ，-8/750 ,（）
A.11/375    B.9/375    C.7/375    D.8/375
解析：把1/5化成5/25
         先把1/5化为5/25，之后不论正负号，从分子看分别是：2，5，8
         即：5-2=3，8-5=3，那么?-8=3
         ？=11
         所以答案是11/375
 
35. 某次数学竞赛共有10道选择题,评分办法是每一题答对一道得4分,答错一道扣1分,不答得0分.设这次竞赛最多有N种可能的成绩,则N应等于多少？
解析：从-10到40中只有
29  33  34  37  38  39
这6个数是无法得到的，所以答案是51-6=45
 
 
36. 1/3 ，1/6 ，1/2 ，2/3 ，（ ）
解析：1/3+1/6=1/2
1/6+1/2=2/3
1/2+2/3=7/6
 
37. N是1，2，3，...1995，1996，1997，的最小公倍数，请回答 N等于多少个2与一个奇数的积？
解析：1到1997中1024=2^10,它所含的2的因数最多，所以最小公倍数中2的因数为10个，所以等于10个2与1个奇数的乘积。
 
38. 5个空瓶可以换1瓶汽水，某班同学喝了161瓶汽水，其中有一些是用喝剩下来的空瓶换的，那么他们至少要买汽水多少瓶？
解析：大致上可以这样想：先买161瓶汽水，喝完以后用这161个空瓶还可以换回32瓶（161÷5=32…1）汽水，然后再把这32瓶汽水退掉，这样一算，就发现实际上只需要买161-32=129瓶汽水。可以检验一下：先买129瓶，喝完后用其中125个空瓶（还剩4个空瓶）去换25瓶汽水，喝完后用25个空瓶可以换5瓶汽水，再喝完后用5个空瓶去换1瓶汽水，最后用这个空瓶和最开始剩下的4个空瓶去再换一瓶汽水，这样总共喝了：129+25+5+1+1=161瓶汽水.
 
 
39. 有两个班的小学生要到少年宫参加活动，但只有一辆车接送。第一班的学生坐车从学校出发的同时，第二班学生开始步行；车到途中某处，让第一班学生下车步行，车立刻返回接第二班学生上车并直接开往少年宫。学生步行速度为每小时4公里，载学生时车速每小时40公里，空车是50公里/小时，学生步行速度是4公里/小时，要使两个班的学生同时到达少年宫，第一班的 学生步行了全程的几分之几？
A.1/7    B.1/6    C.3/4    D.2/5
分析：(A/4)=(B/60)+{(A+5B/6)/40}
A为第一班学生走的，B为坐车走的距离
思路是：第一班学生走的距离的时间=空车返回碰到学生的时间+车到地点的时间
 
40. 甲乙两车同时从A.B两地相向而行，在距B地54千米处相遇，他们各自到达对方车站后立即返回，在距A地42千米处相遇。A.B两地相距多少千米？（提示：相遇时他们行了3个全程）
解析:  设A.B两地相距X千米
两车同时从A.B两地相向而行，在距B地54千米处相遇时,
他们的时间相等, 他们的速度相除为:54/(X—54)
在距A地42千米处相遇时: 他们的速度相除为(X—54+42)/(54+X—42)
他们的速度没有变法, 他们的速度相除值为定量,
所以: 54/(X—54)= (X—54+42)/(54+X—42)
方程式两侧同乘X—54,   54=(X—54) ×(X—12)/(X+12)
方程式两侧同乘(X+12),    54(X+12)= (X—54) (X—12)
                         54X+54×12=X2—54X—12X+54×12
                          X2—66X—54X=0
                          X(X—120)=0
                 X=0(不合题意)   或者说: (X—120)=0     X=120
 
 
41. 3 , 8 , 11 , 9  , 10  , （　）
A.10     B.18     C.16    D.14
解析：答案是A 3, 8, 11, 9, 10, 10=>
3(第一项)×1+5=8(第二项)
3×1+8=11
3×1+6=9
3×1+7=10
3×1+10=10
其中
5、8、6、7、7=>
5+8=6+7
8+6=7+7
 
 
42. 4 ，3 ，1 ，12 ，9 ，3 ，17 ，5 ，( )　　
A.12     B.13     C.14     D.15　　
解析： 本题初看较难，亦乱，但仔细分析，便不难发现，这是一道三个数字为一组的题，在每组数字中，第一个数字是后两个数字之和，即4=3+1，12=9+3，那么依此规律，( )内的数字就是17-5=12。
故本题的正确答案为A。
 
 
43. 地球陆地总面积相当于海洋总面积的41％，北半球的陆地面积相当于其海洋面积的65％，那么，南半球的陆地面积相当于其海洋面积的______％(精确到个位数)．