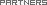?=4×4×4×4×4-4
15620=5×5×5×5×5×5-5
答案是1020 选C
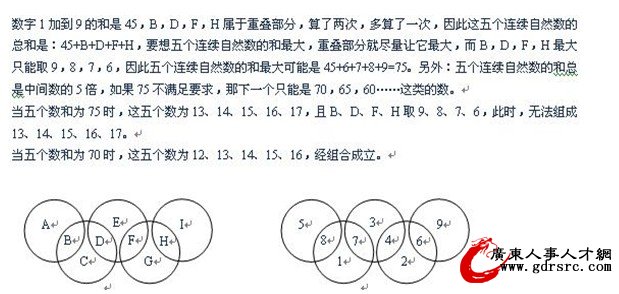
70. 奥运五环标志。这五个环相交成9部分,设A-I,请将数字1—9分别填入这9个部分中,使得这五个环内的数字之和恰好构成5个连续的自然数。那么这5个连续自然数的和的最大值为多少。
A.65 B.75 C.70 D.102
分析:(方法一)题为5个连续自然数,可得出
A+B+1=B+C+D B+C+D+1=D+E+F等.所以求五个连续自然数的和为
5(A+B)+10
H+I最大值为8+9=17,所以A+B<17-4,A+B<13
5(A+B)+10<75
满足5个连续自然数的条件A+B>5+6
5(A+B)+10>65
所以得出答案为70
(方法二)
71. 一水库原有存水量一定,河水每天均匀入库。5台抽水机连续20天可抽干,6台同样的抽水机连续15天可抽干。若要求6天抽干,需要多少台同样的抽水机?
解:水库原有的水与20天流入水可供多少台抽水机抽1天?
20×5=100(台)
水库原有水与15天流入的水可供多少台抽水机抽1天?
6×15=90(台)
每天流入的水可供多少台抽水机抽1天?
(100-90)÷(20-15)=2(台)
原有的水可供多少台抽水机抽1天?
100-20×2=60(台)
若6天抽完,共需抽水机多少台?
60÷6+2=12(台)
72. 甲、乙两车同时从A、B两地相向而行,在距A地80千米处相遇,相遇后两车继续前进,甲车到达B地、乙车到达A地后均立即按原路返回,第二次在距A地60千米处相遇。求A、B两地间的路程。
解析:甲、乙两车从同时出发到第二次相遇,共行驶了3个全程,第一次相遇距A地8O千米,说明行完一个全程时,甲行了8O千米。两车同时出发同时停止,共行了3个全程。说明两车第二次相遇时甲车共行了:80×3=24O(千米),从图中可以看出来甲车实际行了两个全程少60千米,所以A、B两地间的路程就是:
(24O+6O)÷2=150(千米)
可见,解答两次相遇的行程问题的关键就是抓住两次相遇共行三个全程,然后再根据题意抓住第一次相遇点与三个全程的关系即可解答出来。
73. 一名个体运输户承包运输20000只玻璃管,每运输100只可得运费0.80元,如果损坏一只不但不给运费还要赔款0.20元,这位个体运输户共得运输费总数的97.4%,求他共损坏了几只玻璃管?
A.16 B.22 C.18 D.20
分析:20000/100×0.80×97.4%=155.84
0.8×(20000-X/100)-0.2X=155.84
解得X=20
74. 5 , 10 , 26 , 65 , 145 , ( )
A.197 B.226 C.257 D.290
分析:2^2+1=5
3^2+1=10
5^2+1=26
8^2+1=65
12^2+1=145
17^2+1=290
纵向看2、3、5、8、12、17之间的差分别是1、2、3、4、5

76. 65 ,35 ,17 ,3 ,(1) ,1/2
解析:8平方加一,6平方减一,4平方加一,2平方减一,0平方加一, -2平方减一
77. 23 ,89 ,43 ,2 ,(3)
解析取前三个数,分别提取个位和百位的相同公约数列在后面。
78. 假设五个相异正整数的平均数为15,中位数为18,则此五个正整数中的最大数的最大值可能为(C)
A 24
B 32
C 35
D 40
分析(一):因是最大值,故其他数应尽可能小,小的两个数可选1、2,比18大的一个选19,那么用15*5-1-2-18-19可得出这个数为35
分析(二)由题目可知,小于18的2个数字是1和2。所以得到大于18的2个数字和为 75 -18 - 2 - 1 = 54。要求最大可能值,所以另一数是 19 ,最后 最大值 = 54 - 19 = 35 。
79. 3/7 ,5/8 ,5/9 ,8/11 ,7/11 ,()
A.11/14 B.10/13 C.15/17 D.11/12
解析:每一项的分母减去分子,之后分别是:
7-3=4
8-5=3
9-5=4
11-8=3
11-7=4
从以上推论得知:每一项的分母减去分子后形成一个4和3的循环数列,所以
推出下一个循环数必定为3,只有A选项符合要求,故答案为A。
80. 1 ,2 ,4 ,6 ,9 ,( ) ,18
A.11 B.12 C.13 D.14
解析:(1+2+4+6)-2×2=9
(2+4+6+9)-2×4=13
(13+6+9+4)-2×8=18
所以选C
81. 1000个体积为1立方厘米的小立方体,合在一起,成为一个边长为10厘米的大立方体,表面涂油漆后,再分开为原来的小立方体,这些小立方体中至少有一面被油漆涂过的数目是多少个?
解析:最简单的想法就是直接算没有一面被涂的,那就是包含在里面的8×8×8的立方体。个数为:512所以至少涂了一面的为:1000-512=488
答案:488
82. 一种商品,按期望获得50%的利润来定价。结果只销售掉70%商品,为尽早销掉剩下的商品,商店决定按定价打折出售。这样获得的全部利润,是原来所期望利润的82%。问打了几折?
分析:设成本是? 打折率为A
?x0.5x0.7+?x1.5xAx0.3-?X1x0.3=?x0.5x0.82
0.35+0.45A-0.3=0.41 0.45a=0.36 a=0.8
应该是八折
83. 有一条环形公路,周长为2km,甲,乙,丙3人从同一地点同时出发。每人环行2周。现有2辆自行车,乙和丙骑自行车出发,甲步行出发,中途乙和丙下车步行,把自行车留给其他人骑。已知甲步行的速度是每小时5千米,乙和丙步行的速度是每小时4千米,三人骑车的速度都是每小时20千米。请你设计一种走法,使三个人两辆车同时到达终点。那么环行两周最少要用多少分钟
解析:设甲步行x千米,则骑车(4-x)千米,由于乙、丙速度情况均一样,要同时到达,所以乙、丙步行的路程应该一样,设为y千米,则他们骑车均为(4-y)千米。由于三人同时到达,所以用的总之间相等,所以:x/5+(4-x)/20=y/4+(4-y)/20, 得到:y=3x/4. 可以把两个环路看成长为4千米的直线段来考虑,下面设计一种走法:把全程分为三段,分界点为B、C,乙在B点下车,将车放在原地,然后继续走,甲走到B点后骑上乙的车一直到终点,丙骑车到B后面的C点处,下车后步行到终点,乙走到C后骑着丙的车到终点,其中的等量关系可以画线段图解决,我的图贴不上来,所以大家自己画图分析。 设起点为A,终点为D,则可以通过画图找到等量关系:AB=x,BD=4-x,CD=y=3x/4,AC=4-3x/4,BC=y=3x/4,所以有:BD=BC+CD, 即:4-x=3x/4+3x/4, 解得:x=1.6, y=3x/4=1.2. 从而B、C的位置就确定了,时间是:1.6/5+(4-1.6)/20=0.44小时=26分24秒.
84. 用绳子量桥高,在桥上将绳子4折垂至水面,余3米,把绳子3折后,余8米,求桥高是多少米?
分析 :4x+3x4=3x+8x3 x=12
85. 1 ,10 ,3 ,5 ,()
A.11 B.9 C.12 D.4
分析(一):两两相比,1/10,3/5通分,1/10,6/10,下组应该是11/10,故答案A
分析(二):要把数字变成汉字,看笔画1、10、3、5、(4)
一、十、三、五、四
86. 小王有1元、2元、5元、10元面值的邮票,他寄12封信,每封信邮票金额不同,每封信邮票张数要尽可能少,共贴了80元邮票,问:共贴多少张?
解析:贴1张的有4封
贴2张的有
1+2
1+5
2+5
2+2
2+10
贴3张的有
1+2+5
2+2+5
1+2+10
所以共23枚
技巧是要求数额不同,则考虑1,2,3................10,各一封,一共是55元,还有25元,可以拆为14,11各一封,或者12,13各1封,但无论如何拆都要5枚
87. 一只木箱内有白色乒乓球和黄色乒乓球若干个。小明一次取出5个黄球、3个白球,这样操作N次后,白球拿完了,黄球还剩8个;如果换一种取法:每次取出7个黄球、3个白球,这样操作M次后,黄球拿完了,白球还剩24个。问原来木箱内共有乒乓球多少个?
A.246个 B.258个 C.264个 D.272个
解析:三个步骤:
3m-3n=24 m-n=8
(5×8+8)/2=24 m=24
10×24+24=264
88. 1 ,2 ,5 ,29 ,()
A.34 B.846 C.866 D.37
解析:5=2^2+1^2
29=5^2+2^2
( )=29^2+5^2
所以( )=866,选C
89. 1 , 2 , 1 , 6 , 9 , 10 , ( )
A.13 B.12 C.19 D.17
解析:1+2+1=4=2平方
2+1+6=3平方
1+6+9=4平方
6+9+10=5平方
9+10+(?)=6平方
答案:17
90. 1/2 ,1/6 ,1/12 ,1/30 ,( )
A.1/42 B.1/40 C.11/42 D.1/50
解析:主要是分母的规律,2=1×2,6=2×3,12=3×4,30=5×6,?=6×7
所以答案是A
91. 13 , 14 , 16 , 21 ,( ) , 76
A.23 B.35 C.27
解析:按奇偶偶排列,选项中只有22是偶数
92. 1 , 2 , 2 , 6 , 3 , 15 , 3 , 21 , 4 ,( )
A.46 B.20 C.12 D.44
解析:2/1=2
6/2=3
15/3=5
21/3=7
44/4=11